Manipulation de polynômes
Activités #6
Table des matières
1. Représentations en machine des polynômes
- Quelle serait la représentation creuse sous forme de liste du polynôme \(2 + x^ 4 - 3 x^5\) ?
- Et sa représentation dense ?
- Quand choisit-on de travailler plutôt en représentation creuse ?
- Quelle est la représentation la plus économique en terme d’espace mémoire ?
2. Importation du module polynom
Installer le module (une seule fois).
install.packages("polynom")
Utiliser ce module pour vérifier vos résultats.
library("polynom") p1 <- polynomial(c(1,-1,1)) p2 <- polynomial(c(-1,0,1)) ## Affichage print(p1) print(p2) ## Surcharge des opérateurs print(p1+p2) print(p1-p2) ## Évaluations d'un polynome en un point predict(p1,-5:5) ## Visualisation d'un polynome plot(p1, xlim = c(-10,10))
1 - x + x^2 -1 + x^2 -x + 2*x^2 2 - x [1] 31 21 13 7 3 1 1 3 7 13 21
3. Polynômes creux
Vous pouvez vous référer à l’article : sparse polynomial arithmetic.
Un polynôme creux est représenté sous la forme d’une liste de monômes. Un monôme est un vecteur à 2 éléments : (coefficient, degré).
On reprends les deux polynômes p et q utilisés en cours.
p <- list(c(2,5), c(-1,4),c(-2,1)) q <- list(c(1,4), c(7,2),c(-1,0))
3.1. Fonctions utilitaires
- Définir la fonction
is_poly0(p)indiquant si le polynôme est nul. - Définir la fonction
degre(mp)(resp.coeff(mp)) renvoyant le degré (resp. coefficient) d’un monôme ou d’un polynôme. - Programmez la fonction
poly2str(p)renvoyant une chaîne de caractères représentant le polynôme creux sous la forme \(\sum a_i X^i\).poly2str(list()) poly2str(p)
[1] "" [1] "2*X^5 + -1*X^4 + -2*X^1"
- Programmez la fonction
mult_ext(p,k)de multiplication par un scalairekd’un polynôme.poly2str(mult_ext(p,-2))
[1] "-4*X^5 + 2*X^4 + 4*X^1"
3.2. Constructeurs
- Programmez la fonction
make_poly(x)transformant un polynôme plein en un polynôme creux.poly2str(make_poly(c(0, -2, 0, 0, -1, 2))) poly2str(make_poly(c(-1, 0, -7, 0, 1)))
[1] "2*X^5 + -1*X^4 + -2*X^1" [1] "1*X^4 + -7*X^2 + -1*X^0"
- Programmez la fonction
rand_poly(n, coeffs)générant un polynôme aléatoire de degré inférieur ànet dont les coefficients sont tirés dans le vecteurcoeffs.poly2str(rand_poly(5,0:3)) poly2str(rand_poly(10,0:1))
[1] "2*X^3 + 1*X^2 + 1*X^0" [1] "1*X^9 + 1*X^7 + 1*X^5 + 1*X^4 + 1*X^2"
3.3. Addition et soustraction KEY
- Programmez la fonction
add(p,q)d’addition de deux polynômes.Nous allons nous appuyer sur deux fonctions auxiliaires :
- la fonction
sort_monoms(p)qui trie une liste de monômes par degré décroissant ; - la fonction
merge_monoms(p)somme les termes de même degré, et supprime les termes dont le coefficient est nul.
poly2str(add(p, list())) poly2str(add(list(), q)) poly2str(add(p,q))
[1] "2*X^5 + -1*X^4 + -2*X^1" [1] "1*X^4 + 7*X^2 + -1*X^0" [1] "2*X^5 + 7*X^2 + -2*X^1 + -1*X^0"
- la fonction
- Programmez la fonction
sub(p,q)de soustraction de deux polynômes.poly2str(sub(p,p)) poly2str(sub(p,q)) poly2str(sub(q,p))
[1] "" [1] "2*X^5 + -2*X^4 + -7*X^2 + -2*X^1 + 1*X^0" [1] "-2*X^5 + 2*X^4 + 7*X^2 + 2*X^1 + -1*X^0"
## Random list of monoms li <- replicate(10, sample(0:3, 2, replace=TRUE), simplify = FALSE) paste(li) ## Test auxiliary functions p1 <- sort_monoms(li) paste(p1) p1 <- merge_monoms(li) poly2str(p1) p1 <- merge_monoms(append(li, mult_ext(li,-1))) poly2str(p1)
[1] "c(1, 0)" "c(0, 0)" "2:3" "c(0, 0)" "1:2" "c(0, 0)" "2:3" [8] "c(0, 0)" "c(2, 0)" "c(1, 1)" [1] "2:3" "2:3" "1:2" "c(1, 1)" "c(2, 0)" "c(0, 0)" "c(0, 0)" [8] "c(0, 0)" "c(0, 0)" "c(1, 0)" [1] "4*X^3 + 1*X^2 + 1*X^1 + 3*X^0" [1] ""
3.4. Intégration et dérivation
- Programmez la fonction
integ(p)retournant une primitive du polynôme p.poly2str(integ(p)) poly2str(integ(q))
[1] "0.333333333333333*X^6 + -0.2*X^5 + -1*X^2" [1] "0.2*X^5 + 2.33333333333333*X^3 + -1*X^1"
- Programmez la fonction
deriv(p)retournant le polynôme dérivé du polynôme p.poly2str(deriv(p)) poly2str(deriv(q))
[1] "10*X^4 + -4*X^3 + -2*X^0" [1] "4*X^3 + 14*X^1"
3.5. Multiplication interne HARD
Programmez la fonction mult(p,q) de multiplication de deux polynômes. Nous allons nous appuyer sur deux fonctions internes auxiliaires :
- la fonction
mult_monoms(m1, m2)qui multiplie deux monômes. - la fonction
mult_poly_mono(p, m)qui multiplie un polynôme par un monôme.
p1 <- make_poly(c(1,1)) p2 <- make_poly(c(-1,1)) poly2str(p1) poly2str(p2) poly2str(mult(p1,p2)) print("") p3 <- make_poly(c(1,-1,1)) poly2str(p3) poly2str(p3) poly2str(mult(p3,p3))
[1] "1*X^1 + 1*X^0" [1] "1*X^1 + -1*X^0" [1] "1*X^2 + -1*X^0" [1] "" [1] "1*X^2 + -1*X^1 + 1*X^0" [1] "1*X^2 + -1*X^1 + 1*X^0" [1] "1*X^4 + -2*X^3 + 3*X^2 + -2*X^1 + 1*X^0"
3.6. Évaluation d’un polynôme p en un point x. KEY
pn’est pas une fonction, mais on peut toujours créer une fonction associée au polynôme !- Programmez la fonction
polyval(p,x)calculant naïvement \(\sum a_i X^i\).poly2str(p) for(i in -1:1) { print(paste("p(",i,") = ",polyval(p,i), sep="")) } poly2str(q) for(i in -1:1) { print(paste("q(",i,") = ",polyval(q,i), sep="")) }
[1] "2*X^5 + -1*X^4 + -2*X^1" [1] "p(-1) = -1" [1] "p(0) = 0" [1] "p(1) = -1" [1] "1*X^4 + 7*X^2 + -1*X^0" [1] "q(-1) = 7" [1] "q(0) = -1" [1] "q(1) = 7"
- Programmez la fonction
polyhorn(p,x)avec la méthode de Horner.poly2str(p) for(i in -1:1) { print(paste("p(",i,") = ",polyhorn(p,i), sep="")) } poly2str(q) for(i in -1:1) { print(paste("q(",i,") = ",polyhorn(q,i), sep="")) }
[1] "2*X^5 + -1*X^4 + -2*X^1" [1] "p(-1) = -1" [1] "p(0) = 0" [1] "p(1) = -1" [1] "1*X^4 + 7*X^2 + -1*X^0" [1] "q(-1) = 7" [1] "q(0) = -1" [1] "q(1) = 7"
- Comparez les implémentations grâce au code ci-dessous.
x <- seq(2-0.02,2.02,length.out=1001) vec <- c(-2,0,1) ## p(x) = (x^2-2)^16 p1 <- make_poly(vec) for(i in 1:4) { p1 <- mult(p1,p1) } ## Evaluate p using our methods (observed) vn <- sapply(x, polyval, p=p1) vh <- sapply(x, polyhorn, p=p1) library("polynom") ## Evaluate p using R package (expected) pr <-as.polynomial(c(-2,0,1)) ## p is an R object ! I directly used the power operator. pr <- pr ** 16 ## I also use a generic function vr <- predict(pr,x) ## Last, visualize the results cols <- c("red", "gold") matplot(x, cbind(vn-vr,vh-vr),t="l", lwd=2, lty=1,col=cols, xlab="x",ylab="P(x)-P^R(x)") legend("topleft", inset=.05, legend=c("Naive", "Horner"), horiz=TRUE, lwd=2, lty=1, col=cols)
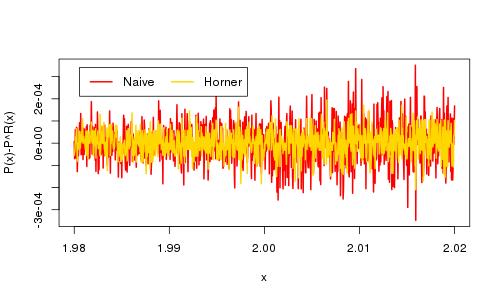
3.7. Visualisation
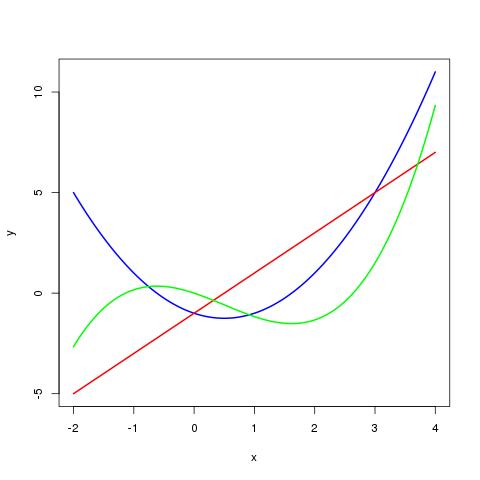
Programmez une fonction dessiner(p,x) sans résultat, chargée de dessiner la courbe du polynôme p (en bleu), ainsi que celles de sa dérivée (en rouge) et de sa primitive (en vert), sur l’intervalle passé en argument.
x <- seq(-2,4,length.out=1000) p1 <- make_poly(c(-1,-1,1)) dessiner(p1,x)
4. Exercice optionnel un peu long, mais intéressant, et ô combien gratifiant !
Reprogrammez complètement le module dans lequel vous opterez pour une représentation dense des polynômes : un polynôme de degré d sera représenté par un vecteur p de longueur d+1 telle que \(a_k=\) p[k+1].