Travaux Pratiques #4
Algo & Prog avec R

Le Modèle de Malthus, dont le nom a donné naissance au malthusianisme, suppose une croissance constante avec un taux \(r\) : \[ N_{t+1} = (1+r)N_t\]

\(r\) représente la différence entre natalité et mortalité: \(r > 0\) indique un surplus de natalité ; \(r \lt 0\) un surplus de mortalité.

Le modèle de Verhulst donnera naissance aux courbes « logistiques » que les biologistes voient si souvent. Il s’écrit comme ceci: \[ N_{t+1} = \left(1 +r\left(1-\frac{N_t}{K}\right)\right)N_t\]

\(r\) a le même sens que précédemment; l’évolution de la population est multipliée par rapport au modèle précédent par \(\left(1-\frac{N_t}{K}\right)\), avec \(K\) la capacité logistique; ce terme tend à devenir faible quand \(N_t\) s’approche de \(K\).

La formule de Newton vu en cours pour améliorer une approximation \(a\) de \(\sqrt{r}\) est obtenue de la manière suivante. On trace la courbe d’équation \(y = f(x) = x^2-r\) qui coupe Ox précisément en \(\sqrt{r}\).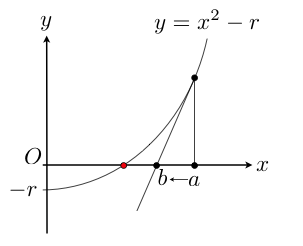

1. Quelle est l’équation de la tangente (T) à la courbe au point d’abscisse \(a\) ?
2. La tangente n’étant pas horizontale, calculez l’abscisse b du point d’intersection de (T) avec Ox. Vous devez retrouver la formule de Newton !

Les calculettes modernes possèdent souvent une touche Solve permettant de calculer une racine d’une équation \(f(x)=0\). Par exemple, il est difficile sans machine de trouver une solution réelle à l’équation \(x^5-3x+1=0\).

1. Pourquoi sommes-nous sûrs qu’il y en a au moins une ?
2. Nous allons faire abstraction de la fonction , la supposer dérivable et à dérivée non nulle en tout point (de sorte que la tangente à la courbe existe et n’est jamais horizontale) pour appliquer la méthode des tangentes de Newton vue ci-dessus dans un cas particulier …

On suppose que l’approximation courante est \(a > 0\). Calculez l’équation de la droite tangente à la courbe de \(f\) au point \((a,f(a))\).

3. Calculez la valeur de \(b\) qui est une amélioration de \(a\).
4. Ecrivez la condition pour que l’approximation courante \(a\) soit suffisamment proche de la solution. On nommera \(h\) la constante > 0 de précision.
5. Ecrivez une expression mathématique utilisant \(f\), \(a\) et \(h\), qui approche la valeur de la dérivée \(f^{\prime}(a)\) de \(f\) au point \(a\).
6. Programmez en R la fonction Solve(f,a,h) retournant une approximation d’une solution de f en partant de l’approximation \(a\). L’argument \(h\) gouvernera la précision.

Solve <- function(f,a,h) {
  ## une solution de f(x) = 0 en partant de a, et h gouverne la precision
  ## tant que la precision n'est pas atteinte...
  while (abs(f(a)) > h)   {
    dfa = (f(a+h)-f(a))/h     # approximation de f'(a)
    a = a - f(a) / dfa        # amelioration de Newton...
  }
  return(a)                      # et hop !
}

g <-function(x) x**5 - 3 * x + 1
sol = Solve(g,1,0.0001)
cat('x**5-3x+1 = 0 admet au moins une racine reelle car le degre est impair, ok ?\n')
cat('Une solution de x**5-3x+1 = 0 :', sol, "\n")
cat('Verification : g(sol) =',g(sol),'où e-05 signifie *10**(-5)\n')

x**5-3x+1 = 0 admet au moins une racine reelle car le degre est impair, ok ?
Une solution de x**5-3x+1 = 0 : 1.214649
Verification : g(sol) = 1.056702e-05 où e-05 signifie *10**(-5)

Utilisez la fonction Solve(f,a,h) pour faire afficher une valeur approchée :

• de \(\sqrt{2}\),
• puis de \(\sqrt[3]{2}\),
• puis d’une solution de l’équation \(x^5-3x+1=0\),
• puis de l’équation \(cos(x)=x\),
• et enfin du nombre \(\pi\).

cat('Approximation de la racine cubique de 2 :',Solve( function(x) x**3-2, 1, 0.0001), "\n")
cat('(la "vraie" valeur est ',2**(1/3),')\n')
cat('Approximation de pi comme solution de sin(x) = 0 :',Solve(sin, 3, 0.0001), "\n")
cat('(la "vraie" valeur est ',pi,')\n')
sol <- Solve(function(x) x-cos(x), 1, 0.0001)
cat('Solution de cos(x) = x :', sol, "\n")
cat('Verification de cos(',sol,') == ', cos(sol), ':', sol == cos(sol), "\n")

Approximation de la racine cubique de 2 : 1.259934
(la "vraie" valeur est  1.259921 )
Approximation de pi comme solution de sin(x) = 0 : 3.141593
(la "vraie" valeur est  3.141593 )
Solution de cos(x) = x : 0.7391132
Verification de cos( 0.7391132 ) ==  0.7390663 : FALSE

N.B. Au moment d’utiliser la fonction Solve(f,a,h), il n’est pas nécessaire que la fonction f soit déjà définie. On peut passer une « fonction anonyme » en paramètre de Solve.

Par exemple, la fonction QUI N’A AUCUN NOM s’écrit en R :

function(x) x**2 – 1

On pourra donc demander par exemple

Solve((function(x) x**2 – 1), 3, 0.01)

Le langage R propose une fonction pour trouver la racine d’une fonction d’une seule variable.

f <- function(x) x**2 - 1
uniroot(f, c(0, 10))

Refaites les applications numériques avec uniroot et comparez les résultats avec ceux de votre fonction Solve.

Écrire une fonction triroot(a,b,c) prenant en paramètre les coefficients a, b et c d’un trinôme et renvoyant les racines réelles de l’équation \(ax^2 + bx + c =0\). Plus précisément, la fonction renvoie :

• NULL si l’équation n’admet pas de racines réelles ;
• un scalaire si l’équation admet une racine double ;

• un vecteur à deux éléments si l’équation admet deux racines distinctes.

  triroot <- function(a, b, c) {
    delta <- b**2 - 4*a*c
    if(delta < 0) {
      return(NULL)
    } else if(delta > 0) {
      s <- sqrt(delta)
      return(c( -b + s, -b - s)/(2*a))
    } else {
      return -b/(2*a)
    }
  }
  

Vérifiez votre programme en utilisant la fonction prédéfinie polyroot.

triroot(1,-3,2)
polyroot(c(2,-3,1))

[1] 2 1
[1] 1+0i 2-0i

Tester votre programme avec le code ci-dessous. Quelle conclusion en tirez-vous?

triroot(0.01,0.2,1)
polyroot(c(1,0.2,0.01))
triroot(0.011025,0.21,1)
polyroot(c(1,0.21,0.01025))

Proposer une amélioration permettant d’éviter le problème ci-dessus grâce à la fonction all.equal.

On va analyser l’erreur d’arrondi pendant le calcul du discriminant quand \(b^2 >> 4ac\) en étudiant le trinôme \(\epsilon x + \frac{x}{\epsilon} - \epsilon\).

li <- head(seq(0.0001,0,length.out=4),-1)
for (epsilon in li) {
  e1 <- epsilon**2
  #cat("Epsilon:", epsilon, "\n"))
  cat("Expected root:",e1, "\n")
  r1 <- triroot(epsilon, 1/epsilon, -epsilon)[1]
  cat("Naive method:",r1, "error=", format(abs(1-r1/e1), digits=3), "\n")
  r2 <-  Re(polyroot(c(-epsilon,1/epsilon,epsilon))[1])
  cat("R method:",r2, "error=", format(abs(1-r2/e1),digits=3), "\n")
}

Expected root: 1e-08
Naive method: 9.094947e-09 error= 0.0905
R method: 1e-08 error= 0
Expected root: 4.444444e-09
Naive method: 1.364242e-08 error= 2.07
R method: 4.444444e-09 error= 0
Expected root: 1.111111e-09
Naive method: 0 error= 1
R method: 1.111111e-09 error= 0

triroot <- function(a, b, c) {
  b <- b/2
  d1 <- b**2
  d2 <- a*c
  if(isTRUE(all.equal(d1,d2))) {
    return(-b/a)
  } else if(d1 < d2) {
    return(NULL)
  } else {
    h <- -(b + sign(b)*sqrt(d1-d2))
    return(c(c/h, h/a))
  }
}

Vous avez de la chance, il existe une classe complex d’emblée intégrée à R, donc sans import.

1. Cherchez dans la documentation ou sur le web comment définir les nombres complexes \(z_1=3-2i\), \(z_2=5+i\) et \(z_3=i\).
2. Calculez l’addition \(z_1 + z_2\), le produit \(z_1 \times z_2\) et l’inverse $\frac{1}{z_3}. Vérifiez que \(z_3\) est bien la racine carrée de -1 …
3. Reprogrammez la méthode triroot retournera aussi les racines complexes.
4. Calculez les racines des polynômes \(2x^2 - 3x -2\), \(x^2+x+1\), et \(x^2+1\).

z1 <- 3-2i
z2 <- 5+1i
z3 <- 1i
z1 + z2
z1 * z2
1/z3

[1] 8-1i
[1] 17-7i
[1] 0-1i