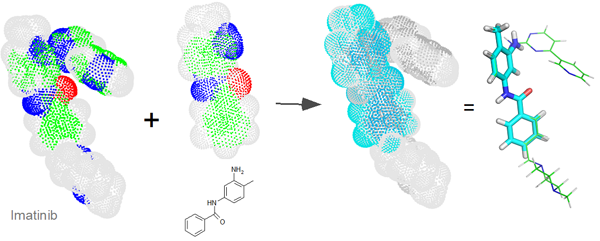
Alignment of 3D molecular structures
Within the framework of an interdisciplinary project initially funded by IDEX JEDI (Academy 4) of University Côte d'Azur, Dominique Douguet (UCA IPMC CNRS INSERM) and Frédéric Payan (UCA I3S CNRS) have developed SENSAAS, an open access software to align 3D molecular structures. Based on their publication publication Shape‐based Alignment by Registration of Colored Point‐based Surfaces available Here in open access, the code is now available on github (github.com/SENSAAS/sensaas), and videos (installation instructions and examples of use) are available on the dedicated channel: https://www.youtube.com/channel/UC3cjM1j8cQ-95ev0DNxRMOA.One Related Publication:sensaas: Shape‐based Alignment by Registration of Colored Point‐based Surfaces has been accepted in Molecular Informatics (Wiley). Authors: Dominique DOUGUET, Frédéric PAYAN. Full Paper (Open Access)